Gender at Birth Ratio

Introduction

Sometime in middle school, I heard a news stating that gender at birth ratio in South Korea has shifted towards having more females. The news stated that change of preference of parents towards having daughters is the reason behind the shift. Abortion, unlike in United States is a rarely talked about topic in Korea and thus I assumed that shift in people’s preference can naturally affect gender at birth ratio. However, I never really thought about the topic until recently at which the results were quite surprising.

Simple Game

Let’s assume that we are doing a coin flipping game on a fair coin. The game is simple. If the coin lands on head, the player earns a dollar. If coin lands tails, the player loses a dollar. The total number of coin flips is set. We can easily argue that the the expected earnings of the player is 0.

Now’s let’s make the game more fun. Now, the player can stop the game at any point. If the player is on a winning streak, the player can leave the game with earnings. Now, let’s look at if there is a strategy that can maximize the player’s earning.

A naive strategy would be to leave the game after the player has more heads than tails. However, quick calculation shows that expected earning of this strategy is 0.

Another naive strategy (and quite popular anecdotally) is to stop when the player hits heads. This, however, also has expected earnings of 0.

Since each coin flip is independent, the expected earnings of the player is 0 regardless of the strategy.

Ratio

Let’s now look at the same game. However, this time, the objective is to maximize the ratio between the number of heads and the number of tails. The player can stop the game at any point.

Concretely, say that the number of heads is \(X\) and number of heads is \(Y\). we want a strategy that maximizes \(\frac{X}{X + Y}\).

You can easily beat the game by stopping the game after the ratio is higher than 0.5. In fact, the calculation shows that the expected ratio \(\approx .74\).

An intuitive picutre is as follows. Let’s say that you had \(A\) heads and \(B\) tails. if \(\frac{A}{A + B} < .5\), then you can always increase the ratio by flipping additional coins.

Interpretation

The above games is a simplification of the gender at birth ratio problem. the number of heads can be thought as number of males and the number of tails can be thought number of females. We have shown that if the coin is fair, there is no strategy to maximize the difference between number of male and female. However, if the objective is to maximize gender at birth ratio, then there exists a strategy that can skew the ratio.

My main question was if the gender at birth ratio can be affected by people’s preference, on large scale.

For a more detailed model, to question if an authoritatively enforced birth ratio policy can affect birth ratio, assuming that gender at birth follows natural gender ratio, we would need to consider the following factors: \(p\): natural gender probability of male birth \(h_k\): number of households with \(k\) being the index. \(m_k\) the number of maximum possible births in household \(k\)

We would want to find some strategy \(S\) that takes in the history of the household births and outputs proceed or stop. This problem seems hard. I asked a statistics professor on this and the response was to first read a book on random walks and then talk. Honestly, I am a computer scientist and is not heavily interested in this topic. So I came up with a simpler simulation and called it a day.

Simulation

A simpler and more efficient method is to simulate random births. The goal of this simulation is to determine the likelihood of achieving a consensus on the birth ratio if the strategy halts successfully at the optimal stopping point.

import random

def max_diff_ratio(min_pop, max_pop, ratio):
    tops = 0
    pops = 0
    
    while pops < min_pop:
        if random.random() < ratio:
            tops += 1
        pops += 1

    max_ratio = tops / pops

    while pops < max_pop:
        if random.random() < ratio:
            tops += 1
        pops += 1

        if tops / pops > max_ratio:
            max_ratio = tops / pops
    
    return max_ratio

We run the above simulation for 10,000 times and show the histogram of the results. I set the min pop to be 1,000,000 max pop to be 1,500,000 and ratio to be 21/41 (natural gender ratio according to Google). Thanks to multiprocessing, the simulation can be done within two minutes.

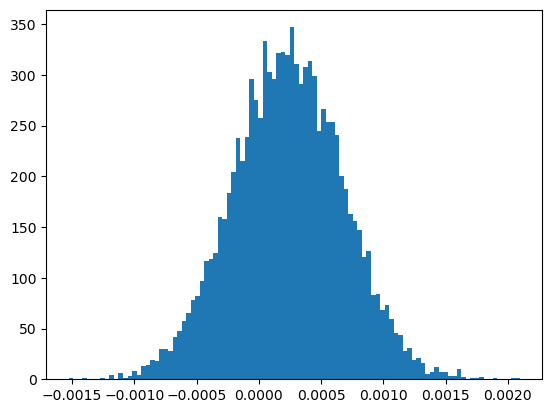
mean: 0.00023

std: 0.00044

results with ratio diff greater than 0.00015: 27

The results show that even with the optimal stopping, changing gender ratio for a large population would not be popssible. There are only 27 cases where the ratio difference is greater than 0.00015. So yeah, if a group of population has gender ratio at birth which greatly differs from the natural, then it is likely that there are other factors at play. (i.e. abortions, gender-selective infections, etc.)