Louvain Clustering

Louvain and Leiden methods are popular for gene clustering. In this post, I will explain the Louvain method.

The Louvain method can be broken into two phases:

1. maximization of modularity: The algorithm tries to maximize the modularity of the graph by moving nodes between communities.
2. aggregation: The algorithm aggregates the nodes in the same community into a single node and creates a new graph.

The two phases are repeated until no further increase in modularity is possible.

First Phase: Maximization of Modularity

The modularity of a graph is defined as

\[Q = \frac{1}{2m} \sum_{i=1}^N \sum_{j=1}^N \left( A_{ij} - \frac{k_i k_j}{2m} \right) \delta(c_i, c_j)\]

Where

• \(A_{ij}\) is the weight of the edge between node \(i\) and node \(j\)
• \(k_i\) and \(k_j\) are the sum of the weights of the edges attached to nodes \(i,j\) respectively
• \(m\) is the sum of all the edge weights in the graph
• \(c_i\) and \(c_j\) are the communities to which the nodes \(i\) and \(j\) belong
• \(\delta\) is the Kronecker delta function:
  • \(\delta(x,y) = 1\) if \(c_i\) and \(c_j\) are the same cluster and 0 otherwise

Modularity lies within range \([-1/2, 1]\).

The modularity above can be written as sum of modularity in a cluster. A modularity of a cluster can be simplified into

\[Q_c = \frac{\sum_{in}}{2m} - \left( \frac{\sum_{tot}}{2m} \right)^2\]

and the total modularity is the sum of the modularity of all clusters.

\[Q = \sum_{c} Q_c\]

Let’s start with basic example of modularity to gain some intuition.

For a graph without any edges, the modularity would be 0.

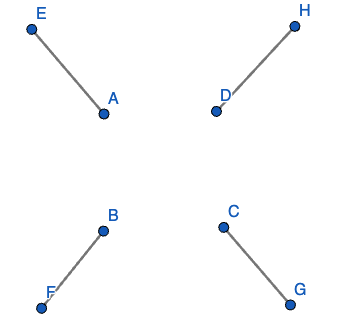
Consider the graph above. Say that we made two clusters, \((A, B, C, D)\) and \((E, F, G, H)\). Then modularity would be

\[(0 - (\frac{4}{8})^2) + (0 - (\frac{4}{8})^2) = -\frac{1}{2}\]

If we define cluster such into \((A,E), (D, H), (B,F), (C,G)\), Then the modularity would be

\[4 \cdot \left(\frac{2}{8} - \left(\frac{2}{8}\right)^2\right) = \frac{3}{4}\]

Now, If we say that the entire graph is one big cluster, we have

\[\frac{1}{8}(8) - \frac{1}{8}(64 \cdot \frac{1}{8}) = 0\]

Finding the optimal clustering is NP-complete hard. so the Louvain method uses a greedy approach. The algorithm does not guarantee the optimal clustering, but it is fast and often gives good results.

The algorithm is as follows:

1. Start with each node in its own cluster.
2. For each node, calculate the change in modularity if the node is moved to a neighboring cluster.
3. Move the node to the cluster that gives the maximum increase in modularity.
4. Repeat steps 2 and 3 until no further increase in modularity is possible.

After the algorithm ends, it is time to move to the second step.

Second Phase: Aggregation

In the second phase, the algorithm aggregates the nodes in the same community into a single node and creates a new graph. The edges between the communities are the sum of the weights of the edges between the nodes in the communities.

Code

What better way to understand the algorithm than to implement it? I have created a simple implementation of the Louvain method in Python. You can find the code here.

Souces

• Louvain Method
• On Modudularity Clustering
• Machine Learning with Graphs Lecture 13.3