Convergence of Minimax complete Binary Tree

Zero-sum games are games where the sum of the payoffs of the players is zero. In other words, the gain of one player is the loss of the other. Examples of zero-sum games include chess, poker, and tic-tac-toe.

The zero-sum games that are turn-based can be represented as a tree. The root of the tree is the initial state of the game. Children of a node show the state of the game after a move. The leaves of the tree are the outcomes of the game. We can assign a value to each leaf node to represent the payoff of the game. The value of the leaf node is positive if the first player wins, and negative if the second player wins.

Also, for a zero-sum turn based 2 player game, the minimax algorithm can be used to find the optimal strategy for both players. Further detail can be found here.

The intuition behind the minimax algorithm is that both players wishes the worst for the other player to maximize their own gain. On odd depth, the first player tries to maximize the value of the node, and on even depth, the second player tries to minimize the value of the node.

Now assume that we know the probability distribution of the outcomes of the game. The question is, if the outcomes of a zero-sum game are equally likely, is the game “fair”?

Just mind that “proofs” in this post are not rigorous.

Simple example

Let’s start with a simple problem. Consider a complete binary tree of depth 2. Furthermore, set the value of the leaf node to be \(0, 1\). An example of such a tree is shown below.

    ?
   / \
  ?   ?
 / \ / \
1  0 1  0

The last player to move in this game is the second player. The second player would choose min of the two possible moves. The updated tree would be

Now, the first player tries to maximize the value of the node.

The value of the root node is 0. This is a winning game for the second player.

We see that if the leaf nodes are chosen, the outcome of the game is deterministic. Also, minimax algorithm starts from the leaf nodes. For formulation of problem, fixing the last player to move is a good choice.

Notations

Let’s now formalize the notations.

For simplicity, we say the min player always moves last. Furthermore, we say that the value of the leaf node is either \(1\) or \(0\) with probability \(p_0\) and \(1 - p_0\) respectively.

We also denote probability \(p_i\) to be that the node is winning in hieght \(i\) to the player on that height.

Binary Randomized Game Tree

Let’s first write a truth table for a min player. The table is shown below.

first node	second node	value
1	1	1
1	-1	-1
-1	1	-1
-1	-1	-1

Now for the max player, the truth table is shown below.

first node	second node	value
1	1	1
1	-1	1
-1	1	1
-1	-1	-1

We see that the truth table is an or. A Node is winning for a player if it is not the case that both of its children are losing for the player. So equation can be written as

\[p_{i + 1} = 1 - p_i^2\]

Furthermore, we also see

\[p_{i + 2} = 1 - (1 - p_i^2)^2\]

Let’s focus on this equation as it captures the change in winning probability of one player.

Properties of the equation.

We first see that if \(p_{i + 2} = p_i\), then \(p_{i + 2k} = p_{i}\). The probability of winning stays constant. For compelte binary tree,

\[p = -p^4 + 2p^2\]

\[p(p - 1)(p^2 + p - 1) = 0\]

The roots are \(0, 1, \frac{-1 \pm \sqrt{5}}{2}\). Probability can only exist between 0 and 1. We aren’t interested in \(\frac{-1 - \sqrt{5}}{2}\). \(0,1\) are trivial. If all the results is winning for one player, then probability of winning is 1.

Now, what can we say about sequences of \(p_i\)?

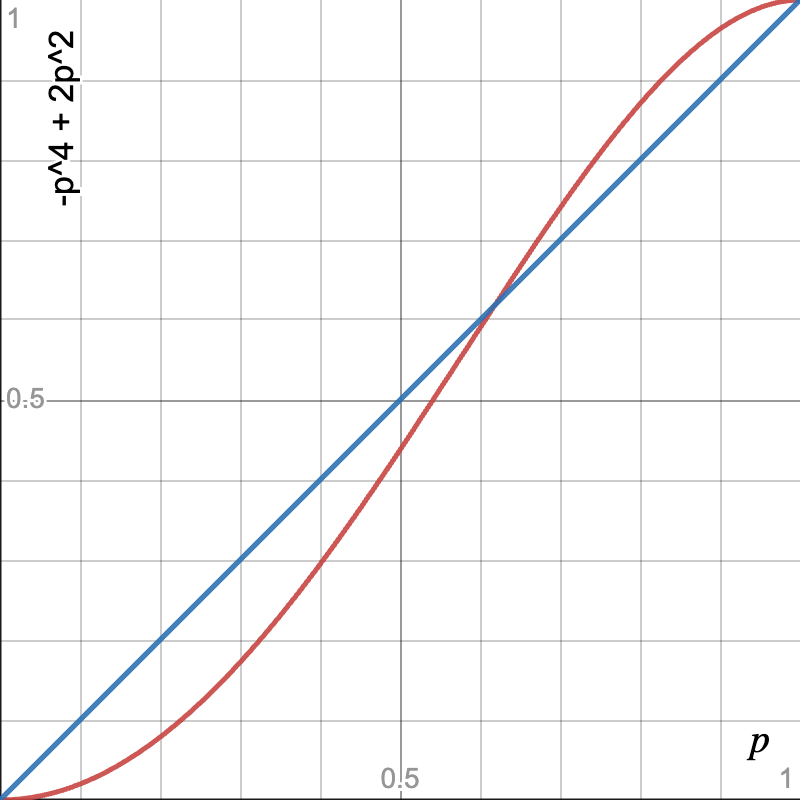
We can draw perpendicular lines to find the values of \(p_{x + 2n}\).

By drawing these lines starting at different initial \(p\) value, we can see that the values tend to \(0\) and \(1\). The sequence only becomes fxed to \(\frac{-1 + \sqrt{5}}{2}\) if the starting probability is \(\frac{-1 + \sqrt{5}}{2}\). These kind of points are called divergent fixed points. Lets define function \(f(p) = 1 - (1 - p^2)^2\).

Proposition: If \(p\) is a fixed point, then iteration diverges if \(f'(p) > 1\) and converges if \(f'(p) < 1\).

So we can check the convergence by checking the values of the derivative. we see tbat \(f'(0) = 0\), \(f'(1) = 0\), \(f'(\frac{-1 + \sqrt{5}}{2}) = 12 - 4\sqrt{5} > 1\). \(0,1\) are convergent fixed points. \(\frac{-1 + \sqrt{5}}{2}\) is a divergent fixed point. So in this case, if \(p_0\) is not \(\frac{-1 + \sqrt{5}}{2}\), then the probability of winning goes to 0 or 1.

An interesting question is the speed of convergence.

Proposition: if \(p_0 < \frac{-1 + \sqrt{5}}{2}\), \(K \in \mathbb{N}\) such that for any \(n \in \mathbb{R}_+\), \(\frac{p_{k + 2}}{p_k} < \frac{1}{n}\) for all even \(k > K\).

Proof

\[\frac{p_{k + 2}}{p_k} = \frac{1 - (1 - p_k^2)^2}{p_k} = \frac{1 - 1 + 2p_k^2 - p_k^4}{p_k} = 2p_k - p_k^3\]

We can show that \(2p_k - p_k^3\) goes to zero as \(k\) increases. Thus the rate of convergence is larger than exponential.

Corollary: Let \(p_0 < \frac{-1 + \sqrt{5}}{2}\). Then there does not exist a \(c \in R_+\) such that for all \(n \in \mathbb{N}\), \(p_{2n} > \frac{1}{c}^n\).

The convergence speed is pretty fast!

Now with other probability distribution

Until now, we have only seen a binary probability distribution: the leaf values were either \(0\) or \(1\). We can show that similar probability holds for any probability distribution on the leaves.

Now, we are more interested in the result of the minimax algorithm.

Proposition: Let a complete binary tree of depth of depth \(n\) with leaf nodes having probability distribution \(p(x)\). Then as \(n\) goes to infinity, Result of the minimax algorithm is \(p(k)\) where \(\int_{-\infty} ^ k p(x) dx = \frac{-1 + \sqrt{5}}{2}\).
Proof: We can think of this problem by binary partition. Let’s say that we partition the distribution above with \(a\) where \(\int_{-\infty} ^a p(x) dx = \frac{1}{2}\). We would have two partitions. Let’s call them \(V_1, V_2\). The probability that the minimax ends with element in partition \(V_1\) is the probability that the outcome is \(0\) when \(p_0 = 0.5\) in the previous problem. From above, we showed that the probability of ending with element in partition \(V_1\) goes to 0. In fact, we see that if the partition is not set at \(p(k)\) where \(\int_{-\infty} ^ k p(x) dx = \frac{-1 + \sqrt{5}}{2}\), then one of probability of elements ending up in partition \(V_k\) goes to \(0\). Thus we can show that the minimax algorithm converges to the partition where \(\int_{-\infty} ^ k p(x) dx = \frac{-1 + \sqrt{5}}{2}\).

I personally thought this was cool.

Next up: Generalization to \(k,l\) tree and more.

Update Logs

Feb 27, 2024: Initial post
Feb 28, 2024: Minor typo fix