Premise

This is part of an ongoing series where I revisit influential papers in NLP. Each post will briefly summarize the core ideas, highlight what I found interesting (or confusing), and sometimes include small experiments. The goal isn’t to be exhaustive.

Attention is All You need (Vaswani et al., 2017)

Many people consider this the landmark paper that ignited the Transformer revolution.

\[\text{Attention}(Q, K, V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V\]

This is the mechanism that started it all.

About Attention Mechanism

The two most commonly used attention functions are additive attention [2], and dot-product (multiplicative) attention. Dot-product attention is identical to our algorithm, except for the scaling factor of \(\sqrt{d_k}\). Additive attention computes the compatibility function using a feed-forward network with a single hidden layer. While the two are similar in theoretical complexity, dot-product attention is much faster and more space-efficient in practice, since it can be implemented using highly optimized matrix multiplication code.

This shows that the idea of attention itself was not new. Previous paper also introduced attention mechanism. It was used as a middle layer connecting encoder and decoder RNNs. The novelty of this paper was showing that attention mechanism alone can be used to replace RNNs.

That said, I think that the title “Attention Is All You Need” is slightly misleading. When I first read the paper, I assumed attention parameters dominated model size. In reality, most parameters come from the feed forward layers (FFN) within each attention block. Most LLMs use 4 times dimension expansion in the FFN layer.

Component	Typical Complexity	Parameter Share
Attention	(O(n^2 d))	~30 %
FFN (MLP)	(O(n d^2))	~70 %

Furthermore, as people, when talking about the complexity, focused on the calculation of the attention weights, which is \((O(n^2 \cdot d))\). However, the feed-forward layers also have complexity of \((O(n \cdot d^2))\), Since in the earlier days of transformers, \(d\) was often larger than \(n\), the feed-forward layers were more computationally expensive on simple tasks.

About Positional Embeddings

The paper introduced sinusodial positional embedding. That is,

\[\text{PE}_{(pos, 2i)} = \sin\left(\frac{pos}{10000^{2i/d_{model}}}\right)\] \[\text{PE}_{(pos, 2i+1)} = \cos\left(\frac{pos}{10000^{2i/d_{model}}}\right)\]

where pos is the position and i is the dimension. That is, each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from 2π to 10000 · 2π. We chose this function because we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset k, \(PE_{pos+k}\) can be represented as a linear function of \(PE_{pos}\)

So what does this mean? Simply, put, we can design a rotational matrix \(\mathbf{R}^k\) such that

\[\mathbf{R}^k \cdot PE_{pos} = PE_{pos+k}\]

Such rotational matrix can be created by the following block diagonal matrix.

\[R_i^k = \begin{pmatrix}\cos k / 10000^{2i/ d_{model}} & -\sin k / 10000^{2i/ d_{model}}\\ \sin k / 10000^{2i/ d_{model}}& \cos k / 10000^{2i/ d_{model}}\end{pmatrix}\] \[\mathbf{R}^k = \begin{pmatrix} R_0 & & & \\ & R_1 & & \\ & & \ddots & \\ & & & R_{d_{model}/2} \end{pmatrix}.\]

This also means position embedding difference between two tokens are determined by its relative distance.

I personally find this formulation elegant but slightly lacking. We can express this as:

\[\mathbf{R}^k \times PE_{pos} + emb = PE_{pos + k} + emb\]

However, the attention mechanism is not additive. It uses dot product attention. Thus the following would have made more sense. Let \(P(x, pos)\) be a function that encodes the position \(pos\) and token embedding \(x\) together. A position encoding should have some function \(\mathbf{F}\) such that

\[\mathbf{F}(P(x,pos), k) = P(x, pos + k)\]

The paper also notes that replacing the sinusoidal embedding with a learnable one barely affects performance.

Simple Experiments

1. Sinusodial Embedding vs Learnable.
2. Additive (Bahdanau-style) vs Dot product attention.

For the base transformer implementation, I used the Andrej Karpathy’s minGPT and evaluated based on the perplexity of the Shakespeare dataset. The code can be found here.

There was a minor difficulty in implementing the Bahdanau Attention. The original attention mechanism in the paper (Which connects encoder with decoder) uses the following

\[\alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{k=1}^{T_x} \exp(e_{ik})} \quad \\ e_{ij} = v_a^T \tanh(W_a s_{i - 1} + U_a h_j)\]

where \(v_a \in \mathbb{R}^n\), \(W_a \in \mathbb{R}^{n \times m}\), \(U_a \in \mathbb{R}^{n \times 2m}\). More detail can be found in the original paper.

To fit this implementation to Transformers, I modified the equation a bit. \(e_{ij} = vx_i\tanh(W_q x_i + W_k x_j)\) Let head size be denoted \(h\). Then, we have \(v \in \mathbb{R}^{h}\), \(W_q \in \mathbb{R}^{h \times h}\), \(W_k \in \mathbb{R}^{h \times h}\).

Notice that \(v\) here is a 1d vector instead of a matrix as in transformer. This was a design choice to be closer to the original Bahdanau attention. The \(q,k\) vectors are same as the original transformer.

But this approach takes up too much memory in parallel computation. We need to materialize matrix of (B, T, T, head_size) tensor to parallelize adding the \(q,k\) vectors. So I used an alternative implementation.

\[e_{ij} = v(\tanh(W_q x_i)) + v(\tanh(W_k x_j))\]

This way, we do not need to materialize the full (B, T, T, head_size) tensor. The two implemtations are not equivalent, but I think this is a reasonable approximation.

Results

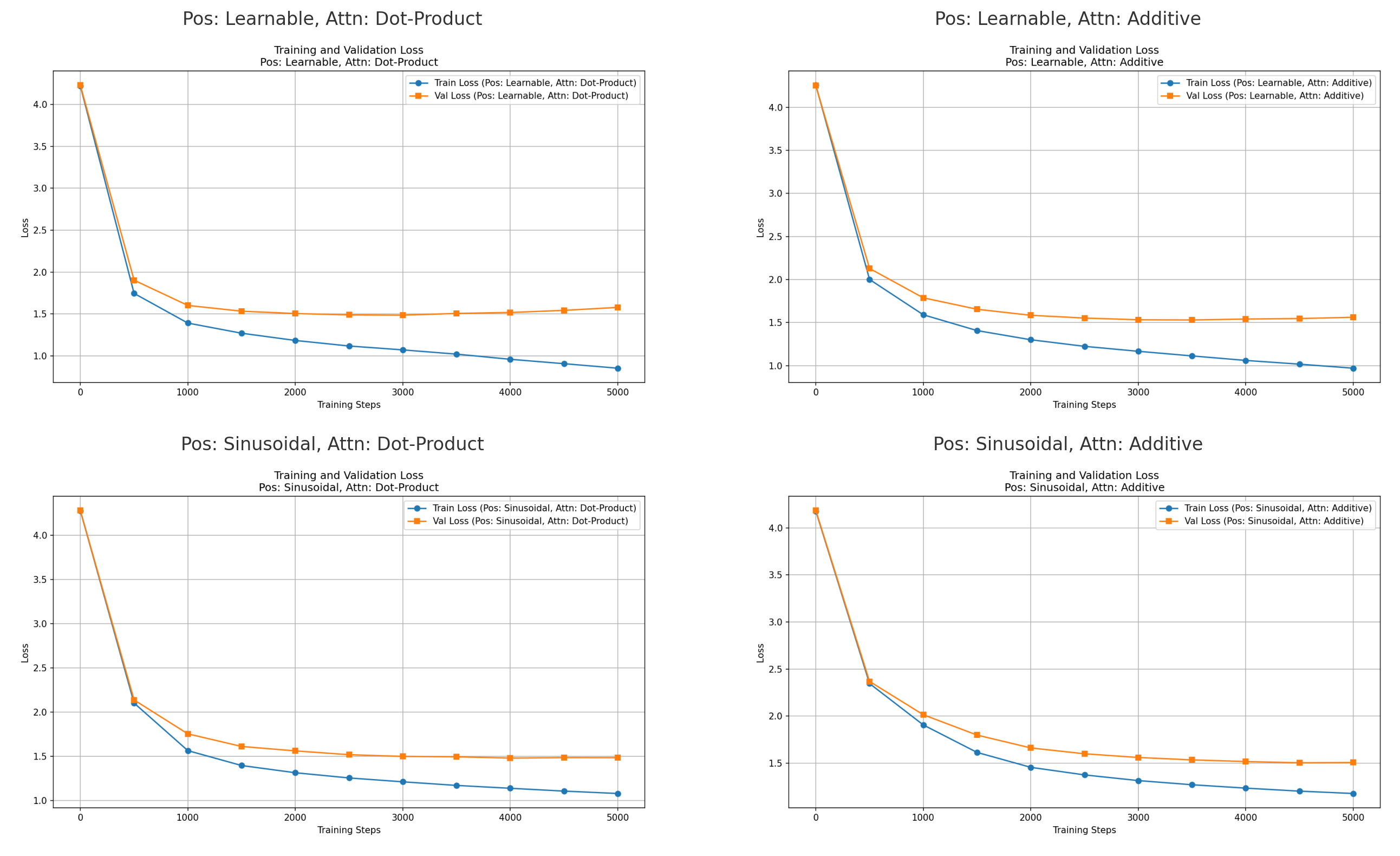
All models produced similar perplexity curves — confirming that both learnable vs. sinusoidal embeddings and additive vs. dot-product attention behave comparably on small datasets.

Takeaways

• Attention wasn’t new — the innovation was using attention-based blocks.
• FFN layers dominate parameters, and sometimes, compute — attention is important, but not the whole story.
• Sinusoidal embeddings are fixed position embedding which allow relative position encoding via rotation.